16 Modélisation statistique : `lm`

Ce document introduit l’aspect le plus basique de modélisation mais qui inspire ou dont dérivent tous les autres : le modèle linéaire aka lm.

Nous allons nous contenter du jeu de données iris et en particulier d’analyser la relation, si elle existe, entre la longueur et la largeur des pétales.

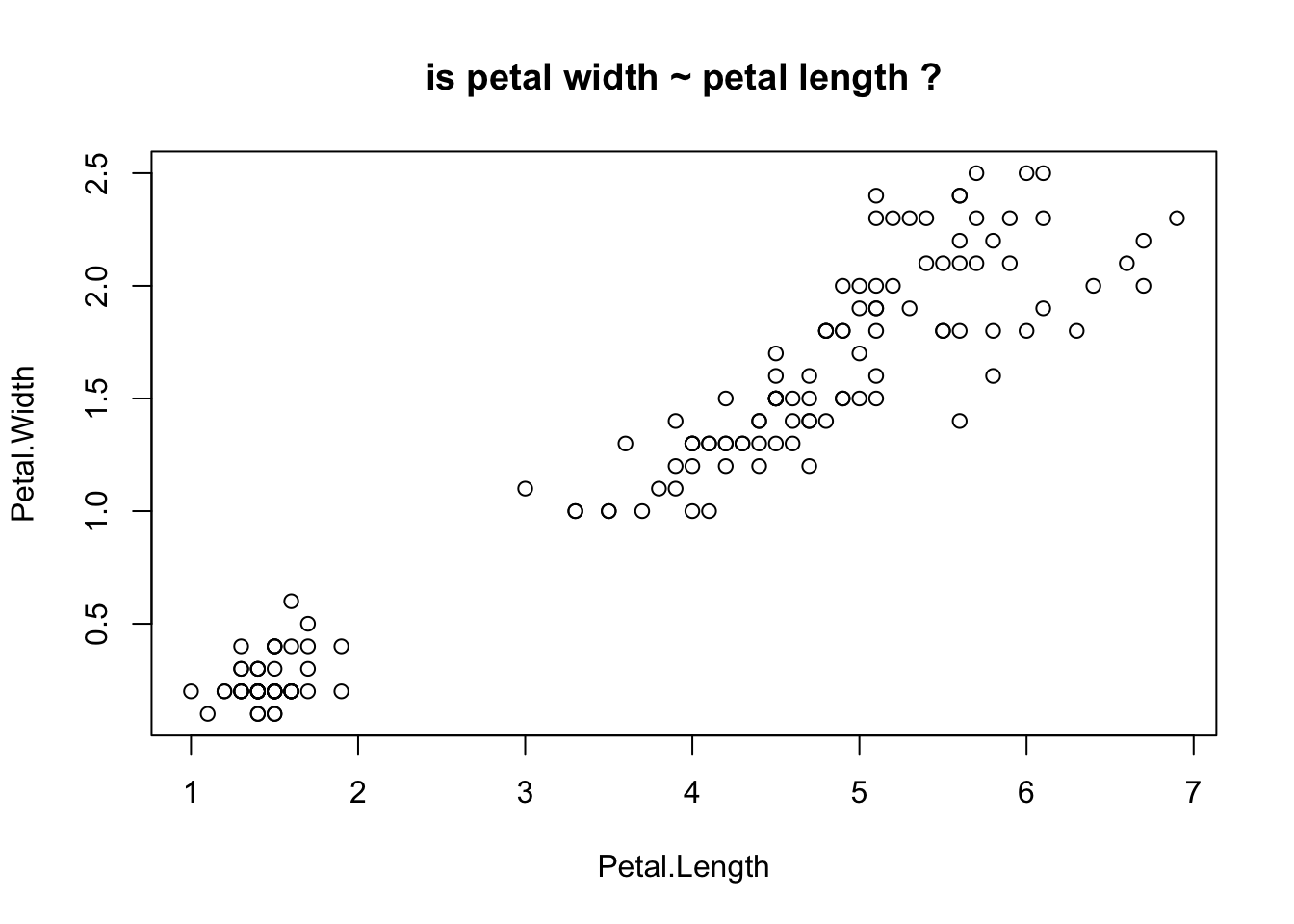
Avant de faire des modèles, faites des graphes !

head(iris)

  Sepal.Length Sepal.Width Petal.Length Petal.Width Species
1          5.1         3.5          1.4         0.2  setosa
2          4.9         3.0          1.4         0.2  setosa
3          4.7         3.2          1.3         0.2  setosa
4          4.6         3.1          1.5         0.2  setosa
5          5.0         3.6          1.4         0.2  setosa
6          5.4         3.9          1.7         0.4  setosa

plot(Petal.Width ~ Petal.Length, data=iris, 
     main="is petal width ~ petal length ?")

mod <- lm(Petal.Width ~ Petal.Length, data=iris)
mod


Call:
lm(formula = Petal.Width ~ Petal.Length, data = iris)

Coefficients:
 (Intercept)  Petal.Length  
     -0.3631        0.4158

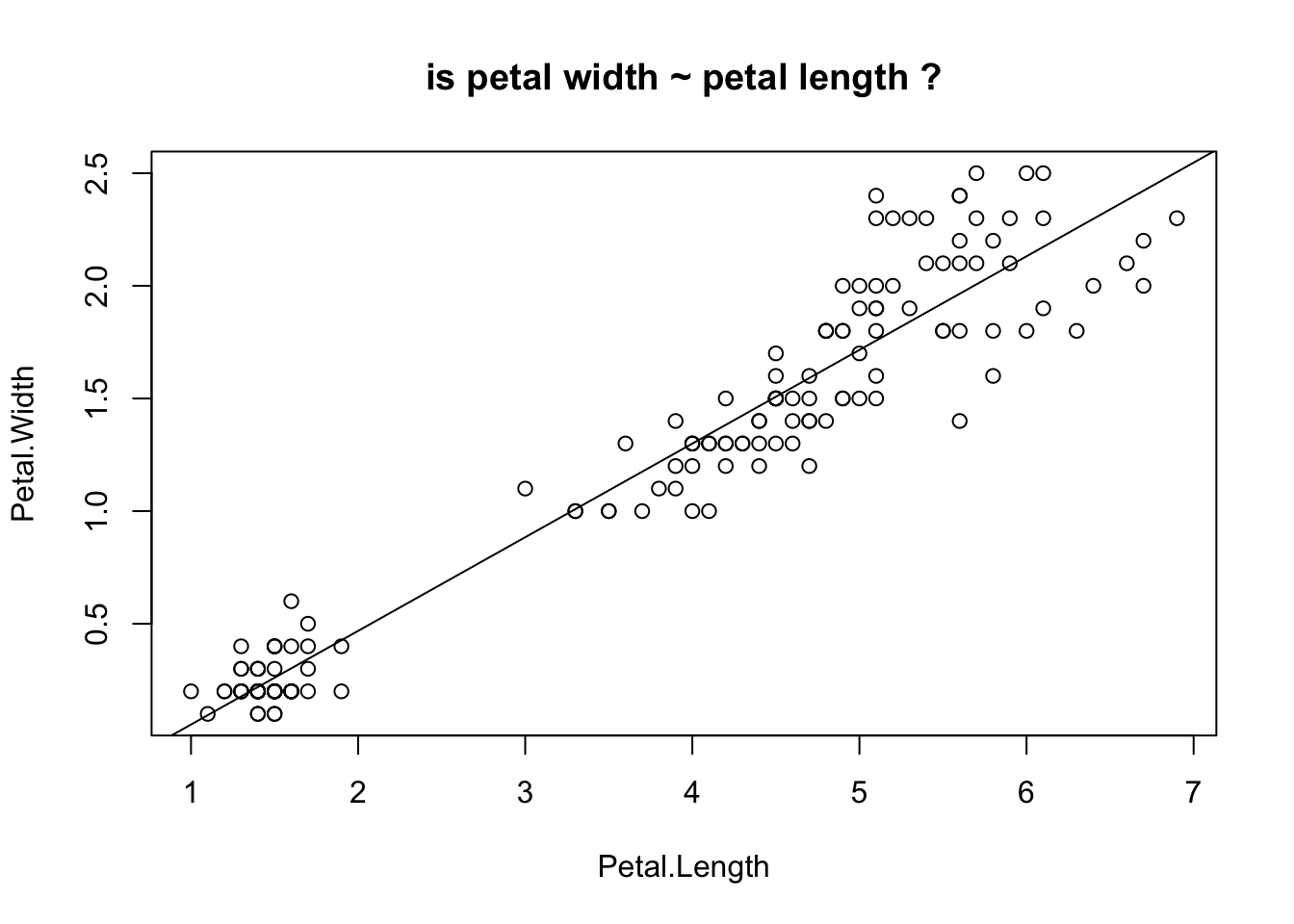
plot(Petal.Width ~ Petal.Length, data=iris, 
     main="is petal width ~ petal length ?")
abline(mod)

summary(mod)


Call:
lm(formula = Petal.Width ~ Petal.Length, data = iris)

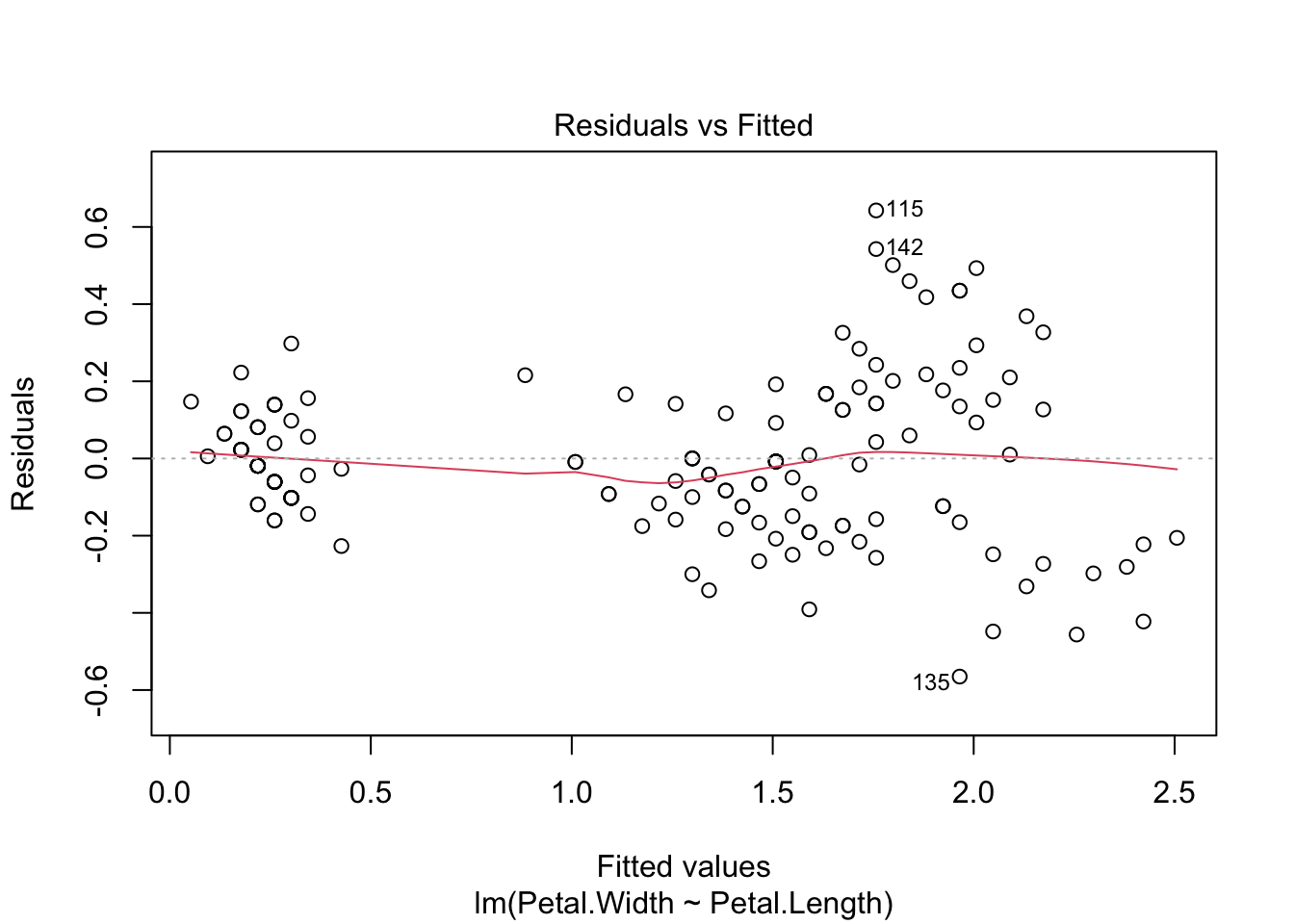
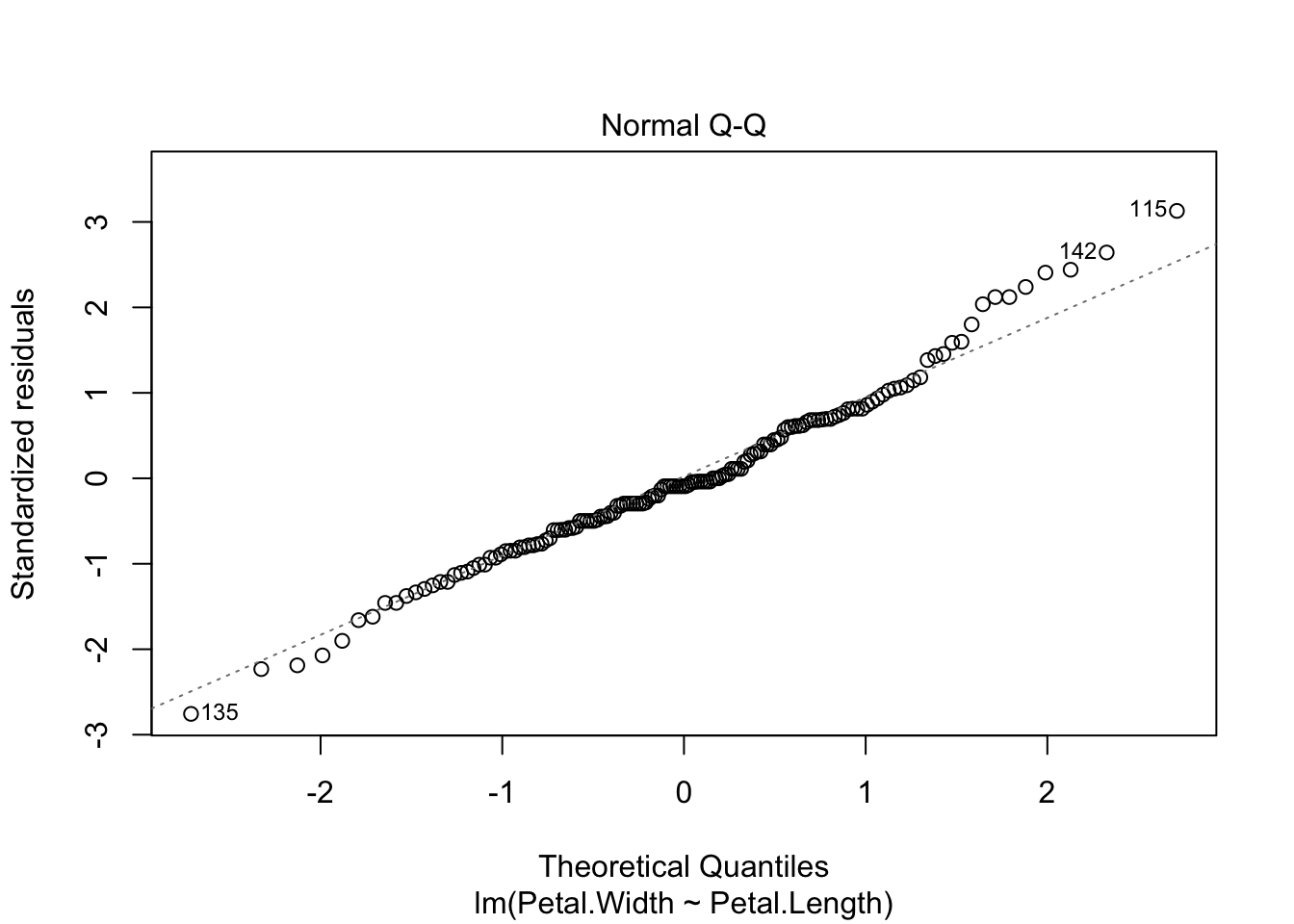
Residuals:
     Min       1Q   Median       3Q      Max 
-0.56515 -0.12358 -0.01898  0.13288  0.64272 

Coefficients:
              Estimate Std. Error t value Pr(>|t|)    
(Intercept)  -0.363076   0.039762  -9.131  4.7e-16 ***
Petal.Length  0.415755   0.009582  43.387  < 2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.2065 on 148 degrees of freedom
Multiple R-squared:  0.9271,    Adjusted R-squared:  0.9266 
F-statistic:  1882 on 1 and 148 DF,  p-value: < 2.2e-16

16.0.1 formula

plot(mod)

#predict()